|
钢桶桶身下料形状精度的确定(2)
三、错位量与对角线之差的关系
(一)对角线之差计算公式推导
前面分析过,错位量主要是因下料呈平行四边形而产生的。那么,错位量与平行四边形对角线之差的关系怎样呢?下面进行论证。
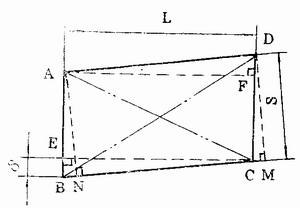
图6
设桶身下料后呈平行四边形ABCD,下料长度为AF=EC=L,宽度为AN=DM=S,两对角线之差|BD-AC|=△,桶身焊缝两端所要求的最大错位量为BE=DF=δ。
在Rt△BMD中
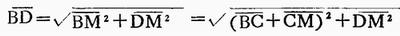
因为在Rt△BEC中
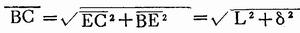
又因Rt△BEC∽Rt△CMD
所以CM=S·δ/L
对角线
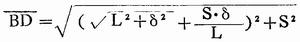
在Rt△ANC中
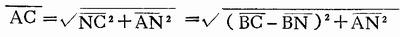
因为△ANB≌△DMC
所以 BN =CM=S·δ/L
AN=DM=S
对角线
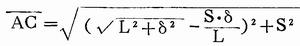
所以两对角线之差计算公式为:
△=|BD-AC|
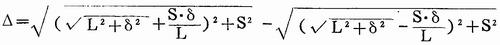
根据上式,当确定了桶身下料长度、宽度和焊缝两端的最大错位量之后,便可求出桶身下料时所要控制的对角线之差,即桶身下料的综合形状精度。
根据上式还可计算出对角线长度的上、下偏差。
标准矩形的对角线长度为: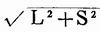 ,那么其上、下俗差分别为: ,那么其上、下俗差分别为:
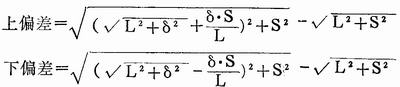
所以对角线长度可表示为:
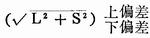
当δ=0时,对角线之差△=0;对角线长度上、下偏差也等于零。这时下料为最理想状态——矩形,但实际中是不存在这种理想状态的。
如图6所示,在实际裁剪时,下料长度一般按平行四边形边长AD(或BC)进行测量。这样测量比较方便,而且AD与AF(或CE)之差微小,可忽略不计,即AD≈AF=L。 同理C≈DM=S, 所以对角线之差计算公式可进行简化。
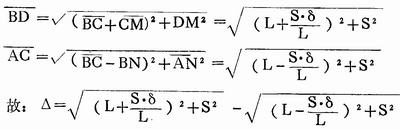
按照上式中的对角线长度公式仍可计算出对角线长度的上、下偏差:
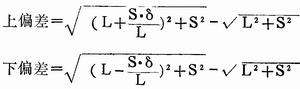
(二)对角线之差计算公式成立的条件
根据前面的分析,对角线之差计算公式成立的条件为:
1.桶身直径和下料长度(或搭边宽度)一定;
2.焊缝与桶身中心轴线平行。
四、用4角的角度偏差确定桶身下料形状精度
前面论证的用对角线之差来确定桶身下料形状精度是为了测量方便而提出的一个综合形状精度指标。在制定工艺和生产中还可控制下料后板料4个角角度偏差来确定形状精度,如图7。
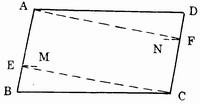
图7
在平行四边形ABCD中,4个角的偏差值都是一样的,只要限制其中一角的偏差,其它三个角也就限制了。
设4个角偏差值为α,下料长度为L,卷边所要求的最大错位量为δ。那么两钝角∠A、∠C为90°+α,两锐角∠B和∠D为90° -α。
在Rt△BEC中, ∠BEC=α, EC=L,BE=δ。
所以
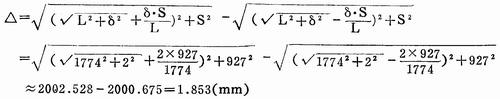
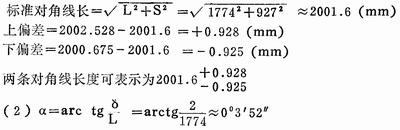
六、小结
通过论证,本文推导出确定桶身下料形状精度的对角线之差和4角角度偏差的计算公式及其与桶身焊缝两端错位量之间的关系。实际上影响错位量和卷边质量的因素是多方面的,本文只是论证丁桶身下料形状精度这一关键因素的影响,使桶身下料形状精度的确定有了理论依据。其它因素对错位量和卷边质量的影响必须在制桶工艺过程的有关环节进行控制。
本文所列公式并通过了一定实际模型的验证,符合公式计算结论。
在本文写作过程中得到了行业相关人士的指导和帮助,在此向他们表示诚挚的谢意。由于本人水平有限,文中难免出现错误,请有关专家和同仁提出宝贵意见。
|

