|
工业包装品回收成本及渠道优化研究(4)-基于Stackelberg博弈的工业包装品回收渠道决策研究
文/金大鑫
4 基于Stackelberg博弈的工业包装品回收渠道决策研究
上文分析了工业包装品回收体系的回收成本,在此基础上,本章重点针对其中的可变成本,研究工业包装品回收渠道的优化问题,使得回收效益最大。以回收体系节省的成本最大为目标,分别建立在生产商回收、需求者回收和第三方回收三种回收渠道下,工业包装品回收体系的经济效益函数,并利用Stackelberg博弈理论分别对各个渠道的效益函数求解,确定合理的回收方案和回收渠道使得包装回收体系的经济效益最大。
4.1 Stackelberg博弈模型分析
4.1.1 模型的定义
工业包装品的回收不是以生产商为主导者,其供应源是包装的拥有者,回收工作可以由供应链上的任何一个参与者进行,其余参与者作为跟随者,所以工业包装品在回收时,存在主从关系,回收主导者可能是拥有包装的零售商、分销商,也可以是工业包装的使用者、生产者,在现代物流中,第三方物流也可以作为回收物流的主导者,任何一方作为回收的主导者都会具有优先权。
Stackelberg博弈是一种具有主从递阶结构的决策问题,它存在两种类型的决策者:处于较高决策层的主导者和处于下级决策层的跟随者,属于完全信息动态博弈理论,博弈过程是透明的,双方的信息都可获取。博弈开始时一般主导者先行动,制定初步策略,然后跟随者根据主导者的策略制定自己最优策略,最后主导者根据跟随者的反应调整自己的行动,最终得出最优策略。这种博弈理论的原理与工业包装品回收情况十分符合。所以本文选择Stackelberg博弈理论来研究工业包装品回收渠道优化选择。
回收渠道有包装生产商渠道、需求者回收渠道和第三方回收渠道三种,分别使用博弈求解出各个渠道下回收体系的最大效益,然后从中决策最优渠道。模型中回收体系的经济效益主要由工业包装品回收节省的成本决定整体经济效益。包装回收过程中,主导者和跟随者相互之间进行各自最大效益的博弈,得出使整体效益最大的供应量,以此求出回收体系的最大效益。模型考虑这些因素,先确定工业包装品回收的主导者,再确定其余追随者。主导者首先确定初步决策,追随者做出相应决策,然后主导者再做出最优决策,并利用Stackelberg博弈理论求解出最大经济效益的表达式。分析比较各个回收渠道的最大效益,确定合理的回收方案使得包装回收体系的经济效益最大,从而决策出最优的回收渠道。
4.1.2 模型参数假设
模型中有多个因素,为方便理解和表达,用参数来代替对应的因素,如下文所述:
Cm:生产商的单位包装生产成本,非负数;
Cm1:生产商可维修的包装单位再造成本,非负数;
Cm2:生产商分解后的包装单位再造成本,非负数;
Cm3:生产商回收完好的包装单位成本,非负数,显然,Cm>Cm2>Cm1>Cm3,说明生产商使用回收的包装进行再造是有直接经济效益的;
Cmr1:回收体系为可维修再造支付给回收者的单位回收价格,非负数;
Cmr2:回收体系为可分解再造支付给回收者的单位回收价格,非负数;
Cmr3:回收体系为回收完好支付给回收者的单位回收价格,非负数;
Pr:工业包装品回收价格,影响回收效益的决策变量,非负数;
Pm:包装批发价格,指生产商向需求者批发包装的价格,为决策变量;
Pn:包装销售价格,指需求者与最终消费者之间的交易价格,为常量;
Qn:工业包装品需求量,包装不同于其他产品,属于附属品,用于包装其他产品,包装的需求量受价格的影响,是销售价格的减函数,故设Qn=a-bPn,其中a和b是由市场需求决定的变数,因工业包装品具有不可缺少性,所以a的值在一定范围内,保证Qn>0;
r:包装回收率,与包装回收价格成正比关系,回收价格越高越能促进回收的积极性,回收率就越高,故设r=kPr,其中k为价格敏感系数,常量;
r1:回收包装的可维修率,即回收后可维修处理重新使用的包装量的比率;
r2:回收包装的可分解率,即回收后可分解处理重新使用的包装量的比率;
r3:回收包装的完好率,即回收后不需再加工直接重新使用的包装量的比率;
Qr:包装回收量,假设等于包装需求量与回收率的乘积,Qr=rQn;
Cri:各种回收渠道下,工业包装品的平均回收成本,包括收集成本、运输成本、分拣成本、库存成本、人工成本等,其中i=m,n,t,依次表示生产商回收、需求者回收和第三方回收渠道,非负数。
在不影响模型的科学性和实用性的前提下,对文中的模型作了一定的假设条件,如下文。
假设1:回收体系中只包含一个生产商、一个需求者和一个第三方回收商。
假设2:回收的工业包装品,分为可直接使用、可维修再造和可分解再造三种情况,除此之外,没有其他的工业包装品废品。
假设3:回收的工业包装品由回收者进行分拣处理,再根据回收包装的质量情况按不同价格转移给包装生产商。
假设4:闭环供应链中的工业包装品回收量加上生产商补充生产的包装量恰好等于下一阶段市场的包装需求量。
假设5:工业包装品回收的可维修率r1、回收可分解率r2和回收完好率r3的值有一定波动,均为区间参数,设R1=[r11,r12],R2=[r21,r22],R3=[r31,r32],其中0≤r11≤r12≤1,0≤r21≤r22≤1,0≤r31≤r32≤1,R1、R2和R3是由回收商根据回收包装的信息分析得出的,且在闭环供应链中是共享的。
假设6:λ1、λ2、λ3表示生产商、需求者和第三方回收商实施工业包装品回收过程中追求经济效益最大时承担的风险程度,包括成本风险、对主营业务造成影响的风险、对总体经济效益造成的风险等。由于回收可维修率、可分解率和完好率为区间参数,因而决策者的目标函数也在一定区间[X1,X2]内变化,根据相关研究,目标函数可以转化为λX2+(1-λ)X1。
假设7:f表示工业包装品回收体系进行包装回收再造时平均节省的生产成本,用可维修再造成本、可分解再造成本和回收完好成本的函数式表示,记f=Cm-Cm1R1-Cm2R2-Cm3R3,f为区间参数,设f=[f1,f2],记f*=λ1f2+(1-λ1)f1,表示回收体系在风险系数λ1情形下进行再制造平均节省的成本。
假设8:h表示回收体系支付给工业包装品回收者的平均价格补贴,记h=Cmr1R1+Cmr2R2+Cmr3R3,h为区间参数,设h=[h1,h2],记h*=λh2+(1-λ)h1,表示回收者在风险系数λ下获得的平均价格补贴。
4.2 生产商回收渠道下的回收模型研究
4.2.1 模型构建
在这种回收渠道下,参与者包括生产商、需求者和最终客户,生产商负责产品的生产、回收和再制造工作,需求者负责包装的采购和使用。博弈发生在生产商和需求者之间,根据Stackelberg博弈理论,在包装回收的闭环供应链中,生产商处于主导者的地位,需求者处于追随者地位,并且彼此之间的信息是对称的,则在博弈中,处于主导者的生产商首先确定工业包装品的批发价格,需求者依据生产商确定的批发价格调整销售价格,之后生产商根据需求者的反应再做出决策,确定最优回收价格。
生产商的经济效益由两部分组成,批发包装的经济效益和使用回收包装进行再制造带来的经济效益,设生产商的经济效益为Em,需求者的经济效益主要是销售包装获得的,设为En。下面分别建立各参与者的经济效益模型。
生产商批发包装的经济效益为Qn(Pm-Cm),使用回收包装再造带来的经济效益等于回收节省的成本减去回收所需的成本,节省的成本由f*可得,回收所有成本由Pr和Crm可得,所以回收包装再造带来的经济效益为Qr[f*-(Pr+Crm)],则生产商的经济效益为:
Em=Qn(Pm-Cm)+Qr[f*-(Pr+Crm)] (4.1)
需求者的经济效益由销售获得,其经济效益为:
En=Qn(Pn-Pm) (4.2)
回收体系的经济效益包含所有的回收参与者的整个回收供应链的经济效益,由包装回收节省的成本组成,经济效益为:
Em=Qr(f*-Pr-Crm) (4.3)
4.2.2 模型求解
结合Stackelberg博弈理论,生产商处于主导者时,先确定生产商的最优价格,再使需求者经济效益最大化,然后生产商根据需求者的变动调整方案,使得经济效益最大化。将Qn,Υ和Qr的表达式分别带入到以上公式中,然后将(4.2)式对销售价格Pn求偏导数,并令其等于零。
即∂En/∂Pn=0,可求得
Pn=(a+bPm)/2b (4.4)
故
Qn=(a-bPm)/2 (4.5)
将(4.4)和(4.5)代入(4.1)中,对Pr和Pm分别求偏导数,可求得
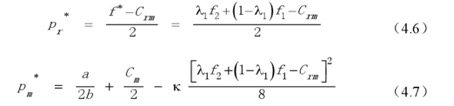
根据以上求解的值,可得出
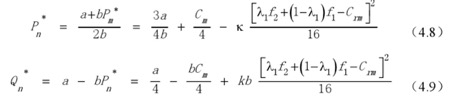
因为回收价格是影响回收效益的决策变量,将回收体系的效益模型对回收价格求一阶偏导数,可得∂Em/∂Pr=(f*-Crm-2Pr)kQn,令其等于零,可得∂Em/∂Pr=(f*-Crm-2Pr)kQn,令其等于零,可得
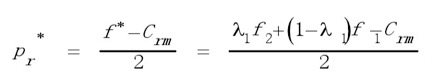 。 。
再将回收体系效益模型对回收价格求二阶偏导数,可得
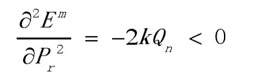 (4.10) (4.10)
说明回收体系在最优回收价格Pr处得到极大值。
分析表明,工业包装品回收体系的经济效益在最优回收价格处能够获得最大值的。
将上式(4.6)至(4.9)代入到(4.3)中,得出工业包装品回收体系的最大(或者最小)经济效益为:
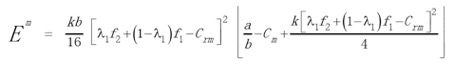 (4.11) (4.11)
需要说明的是,回收体系具体经济效益有两个前提,一是工业包装品回收体系进行包装回收再造时平均节省的生产成本要大于回收成本,即λ1f2+(1-λ1)f1>Crm。第二,包装需求量变数比值要大于包装生产成本,即 a/b>Cm,这就表明,包装需求量必须达到一定规模,回收才有经济效益。
4.3 需求者回收渠道下的回收模型研究
4.3.1 模型构建
在需求者回收渠道下,生产商负责工业包装品的生产和回收后的再制造,需求者负责工业包装品的销售和回收,并对回收的包装进行收集、分拣、运输等处理。生产商是包装回收的主导者,需求者是追随者,博弈发生在生产商和需求者之间。
在这种回收渠道下,生产商的经济效益由批发包装和再制造带来的经济效益组成,需求者的经济效益由销售和回收价格补贴组成,设生产商的经济效益为Emn,需求者的经济效益为Enn,回收体系的经济效益为En。
生产商批发包装的经济效益为Qn(Pm-Cm),使用回收包装再造带来的经济效益等于再制造节省的成本减去支付给回收者的价格补贴,由上文假设可知,节省的成本f*,支付给回收者的价格补贴为h*,则生产商的经济效益为:
Enm=Qn(Pm-Cm)+Qr(f*-h*) (4.12)
需求者销售经济效益为Qn(Pn-Pm),回收价格补贴经济效益等于获得的补贴减去回收的所有成本,包括从最终包装消费者回收支付的成本Pr和自身运营成本Crm,那么需求者的经济效益为:
Enn=Qr(h*-Pr-Crn) (4.14)
4.3.2 模型求解
在Stackelberg博弈应用中,生产商处于主导者,生产商最先确定初步的批发价格和回收价格补贴,需求者对于生产商给定的批发价格和回收价格补贴做出最佳决策,然后生产商据此调整策略达到最优。
假设需求者回收的风险系数为λ2,根据前文假设内容可以得出需求者获得的回收价格补贴h*=λ2h2+(1-λ2)h1。
先使需求者追求经济效益最大化,将Qn、γ和Qr的表达式分别带入到以上公式(4.11)(4.12)和(4.13)中,然后将(4.12)式对回收价格和销售价格Pn求偏导数,并令其等于零。
即令∂Emn/∂Pr=0,∂Emn/∂Pn=0,可求得
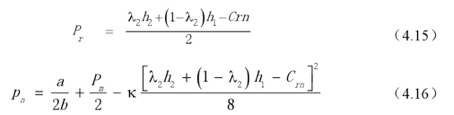
再将以上两个式子代入到式(4.11)中,将生产商的经济效益函数对包装批发价格和回收价格求偏导数,可求得
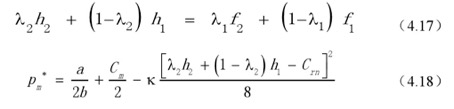
则有
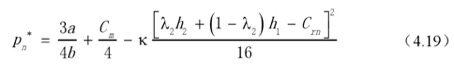
与生产商回收渠道相同,可以分析出回收体系的经济效益在最优回收价格处获得最大值。
将上式(4.14)至(4.18)代入到(4.13)中,便可求得需求者回收渠道下回收体系的最大(或最小)经济效益,为:
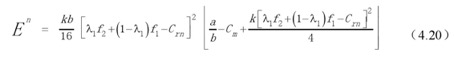
4.4 第三方回收渠道下的回收模型研究
4.4.1 模型构建
在第三方回收商回收渠道下,生产商只负责工业包装品的生产和再制造,需求者只负责采购和使用,第三方回收商负责包装的回收,并对包装进行收集、分拣、运输等处理,并且根据回收质量的不同以不同的价格转让给包装生产商,生产商对回收包装再制造后进行批发销售。生产商依然是回收的主导者,需求者和第三方回收商是追随者,博弈发生在生产商与需求者、第三方之间。
在这种回收渠道下,生产商的经济效益由批发包装的经济效益和回收包装再制造带来的经济效益组成,需求者的经济效益由销售获得,第三方的经济效益完全由回收价格补贴获得,回收体系的经济效益由包装销售带来的经济效益和回收节省的成本组成。设生产商的经济效益为Emt,需求者的经济效益为Ent,第三方回收商的经济效益为Ett,工业包装品回收体系的经济效益为Et,如下文分析。
生产商批发工业包装品的经济效益为Qn=(Pm-Cm),包装回收的经济效益由再制造节省的成本减去支付给第三方回收商的成本,节省的成本由f*的函数式表示,支付成本由h*的函数式表示,所以生产商的经济效益为:
Emt=Qn(Pm-Cm)+Qr(f*-h*) (4.21)
需求者的经济效益还是由销售所得:
Emt=Qn(Pn-Pm) (4.22)
第三方回收商的经济效益由获得的回收价格补贴减去回收所有的成本所得,价格补贴由h*的函数式表示,回收的成本包括支付给最终包装消费者的成本Pr和自身的运营成本Crt,则第三方回收商的经济效益为:
Ett=Qr(h*-Pr-Crt) (4.23)
工业包装品回收体系的经济效益由包装回收节省的成本组成,与上文类似,回收体系的整体经济效益为:
Et=Qr(f*-Pr-Crt) (4.24)
4.4.2 模型求解
与前文相同,先使需求者和第三方经济效益最大化,再使生产商经济效益最大化,最后求得最优解。
设第三方回收商从生产商处获得的回收价格补贴为h*=λ3h2+(1-λ3)h1,其中λ3为第三方回收商的风险系数。
将Qn、Υ和Qr的表达式代入式(4.20)至(4.22)中,然后将式(4.21)对销售价格Pn求偏导数。
即∂Ett/∂Pm=0,可求得

将求得的Pn和Qn代入到式(4.22)中,并对其求回收价格的偏导数
即∂Ett/∂Pr=0,可求得
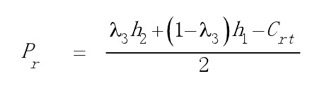 (4.27) (4.27)
再将求得的Pr代入到式(4.20)中,将生产商的经济效益函数对包装批发价格和包装回收价格求偏导数,可求得
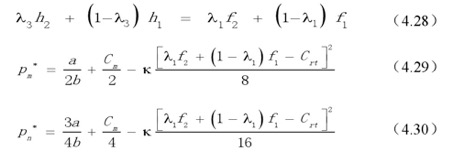
与上文类似,可以分析出回收体系的经济效益在最优回收价格处获得最大值。将求得的Pm*和Pn*代入到式(4.22)和(4.23)中可计算得出第三方回收商的经济效益和回收体系的最大(或最小)经济效益。
第三方回收商的经济效益为:
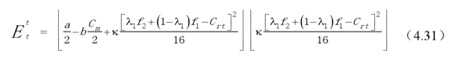
回收体系的最大(或最小)经济效益为:
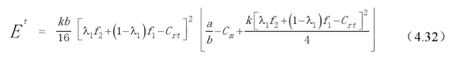
4.5 模型结论
综合以上研究可知,不同回收渠道下,工业包装品回收体系的回收效益不同,生产商回收渠道、需求者回收渠道和第三方回收渠道下回收体系的经济效益各不相同,具体情况统计如下表4.1所示:
表4.1 不同回收渠道的回收效益
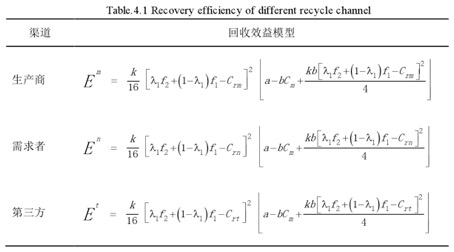
从这个表中,可以看出工业包装品回收体系的经济效益受一些条件的影响,主要是回收再造的成本节省、回收成本、包装需求量、包装生产成本等,具体分析如下。
① 回收再造节省成本
回收体系的经济效益模型中,回收再造节省的成本用λ1f2+(1-λ1)f1表示,指回收体系中的包装生产商通过对回收的包装进行再造比生产新包装减少的成本。从上述回收效益模型中,分析得出,回收再造节省的成本必须大于回收产生的成本,回收才会有经济效益,否则回收是亏损的,即满足λ1f2+(1-λ1)f1>Cri,其中,Cri分别表示生产商回收渠道、需求者回收渠道和第三方回收渠道的回收成本,包括收集成本、分拣成本、清洗成本、运输成本、人工成本等。不同的回收渠道下回收成本不同,直接影响回收体系是否具有经济效益。
② 需求量与回收量
在工业包装品的回收体系中,另外一个制约回收效益的要素是包装的需求量。反映在上面的效益模型中,就是a>bCm。其中,a和b是由包装市场需求决定的变数,反映的是包装的需求情况。同时,包装的回收量等于需求量乘以回收率,其中回收率是定值,所以包装的需求量直接决定了包装的回收量。可以这样定性的理解,当包装的回收量较小时,回收花费的成本平均到每个回收包装上的费用高于回收再造节省的成本,这时回收是没有经济效益的。当包装的回收量达到一定规模后,平均到每个回收包装的回收成本小于回收再造节省的成本,这时回收具有经济效益。所以只有在需求量和回收量达到一定规模后,工业包装品回收体系才会有经济效益。
③ 回收成本
由上表可知,回收体系的经济效益与回收渠道的回收成本成反比关系,而且,前文研究得出,工业包装品回收体系在最优回收价格处获得最大经济效益,而计算得出,最优回收价格等于回收体系回收再造节省的成本减去回收成本的差值的一半,所以最优回收价格受回收成本影响,回收体系的经济效益也由回收成本决定。不同的回收渠道下,回收成本大小不同,所以,选择合适的回收渠道,对于回收体系的的效益影响重大。
综合以上分析,工业包装品回收体系的经济效益与回收再造节省成本、回收量、回收成本直接相关,不同的回收渠道下,回收量、回收成本不同,所以选择合适的回收渠道对于回收体系的效益影响重大。当回收渠道的回收再造平均节省的生产成本大于回收成本,回收量达到一定规模时,回收体系才有经济效益,再比较不同渠道下回收体系的经济效益,决策出最优的工业包装品回收渠道。
4.6 本章小结
本章节首先对回收渠道优化研究模型进行了定义,对模型中涉及到的参数和约束条件进行了假设,然后分别研究了在生产商回收、需求者回收和第三方回收三种回收渠道下,工业包装品回收体系的经济效益模型,并使用Stackelberg博弈理论进行求解,最后分析得出研究结论。
【相关链接】
工业包装品回收成本及渠道优化研究(1)-绪论
工业包装品回收成本及渠道优化研究(2)-工业包装品回收理论及现状研究
工业包装品回收成本及渠道优化研究(3)-工业包装品回收体系构建及成本研究
工业包装品回收成本及渠道优化研究(4)-基于 Stackelberg 博弈的工业包装品回收渠道决策研究
工业包装品回收成本及渠道优化研究(5)-实证研究——以C公司托盘回收为例
工业包装品回收成本及渠道优化研究(6)-总结与展望
|

